understanding Binary Numbers Explained

Read Time:5 Minute, 30 Second

In my whole teaching life, I have noticed that most of my students struggle and fight with IP addresses.

Why this happen? It happens because of the lack of understanding of the binary numbers. It is essential to have a basic understanding of binary numbers and the understanding to find the difference between binary and decimal numbers.

It is an essential part of the subject that must be known to all of you. You should also have a flair understanding of coding, networking and other vital parts.

Binary 101:

In this part, you will learn about some essential parts and they are

The bases of number that include Base 10, Base 2 and Base 16.
The process of converting binary to decimal and vice versa.
The process of converting binary to hexadecimal and vice versa.
The process of converting hexadecimal to decimal and vice versa.

A complete overview of Base 10 system:

It must be known to all that the principles are always the same for all the numbers. At first, the decimal system uses 10 as a base and so the number ranges from 0 to 9. Let’s have a look at some of the examples.

Let us commence with a three-digit number as 129. It is made as 100+20+9=129.

Now if you have a glance at the below diagram you will find that we move from right to left and the columns increase by 10. Just have a look at the below diagram.

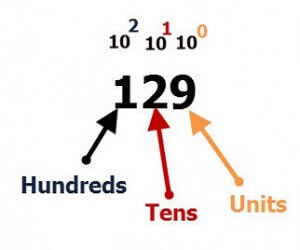
Again there is a short table that will be shown below. This will also make the whole thing clear to the users.

At the time of writing decimal numbers we never write columns. This is because we know that they are simple to write. It is written as,

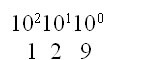
The concept of power notation is introduced because it is essential to write the binary numbers.

The minimum possible three digit number is 000 and the maximum one is 999. If the number is larger than 999 we write is as 1000.

All about binary number system:

You must remember that binary numbers are base 2 numbers. They have only two values and they are 0 and 1.

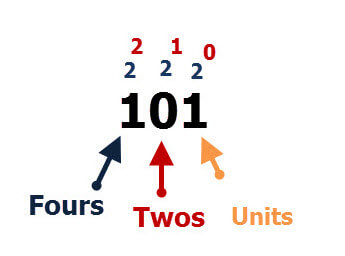
But again if we have a look at the binary numbers such as 101 we have to assign columns. Now we will use 2 and not 10 as the base.

So, ultimately binary 101 has 1 units in one column,0 in the 2 columns and 1 in the 4 columns. Now here we also work from right to left.

Below you will get a picture or a diagram that will make everything clear.

On the other hand, binary numbers use base 2 and so the columns appear as

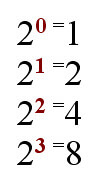
Process of conversion from binary to decimal:

Let’s take some binary numbers and convert it to the decimals. Let us start with three digit binary number 101.

1*1 + 0*2 + 1*4 = 5

The maximum values that one can have with binary numbers or digits are 111=decimal 7 are calculated as follows. 1*1 + 1*2 + 1*4

Some more examples are provided below.

1011 binary = 1*1+1*2+0*4+1*8=11

1111 binary = 1*1+1*2+1*4+1*8=15

Process of conversion from decimal to binary:

Now what is the actual process of converting decimals to binary. In the next few steps you will know about the whole process.

The way I do it is by using the following list of 2 multiples.

128, 64, 32,16,8,4,2,1

You can also follow a handy chart. Here comes it.

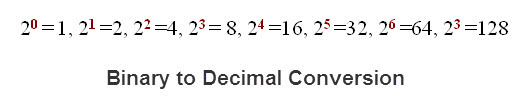
The procedure of doing thisis to subtract the number with largest power of two from the decimal number

The largest power of two number and that we can subtract is 8 which is 2³.

So 10-8 =2

Now we can do the same with the remainder so the largest number we can subtract is 2 which is =2¹

2-2=0

So we have 1 eight , No fours, 1 two, No units = 1010 = 2³+ 2¹.

Example 2: Decimal 13 to binary code

1 eight , 1 four, 0 two, 1 units = 1101.

Example 3: Decimal 7 to binary code

0 eight, 1 four, 1 two, 1 units = 0111.

Answers to try it yourself questions

1001 binary = 9

1100 binary = 12

Bytes and Octets and Hexadecimal Numbers

In computer language both coding and networking 8 bit numbers are commonly found.

An 8 bit number is known by the name of octet, and sometimes it is called a byte. You can also visit other sites to collect more information..

Binary to Decimal and vice versa Conversion 8 Bit Numbers

An 8 bit binary number can be represented with a maximum of decimal 255= binary 11111111.

It is calculated as follows:

1*128 +1*64+1*32+1*16+1*8+1*4+1*2+1+1 = decimal 255

Here is another 8 bit binary number –01101011.

For converting the numbers to decimal you can write the number along with the column numbers above, just as follows:

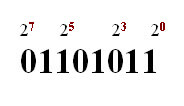
Suppose, if you convert the columns to decimal equivalents by following the chart.

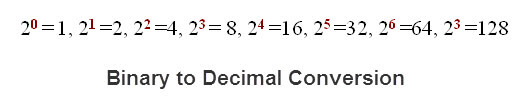
Now the binary number 01101011 = 1*1 +1*2+0*4=1*8+0*16=1*32+1*64+0*128

=64+32+8+2+1= 107

You must know it well that it consists purely of 1’s and 0’s.

While converting this number into decimal you require to understand what each 1 signifies.

If the column values are written normally above the numbers then it will become easy and smooth to convert the binary number to decimal.

Decimal to Binary Conversion Example

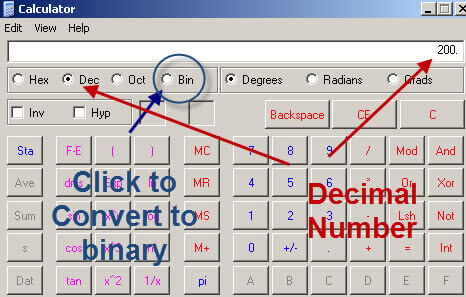
Now comes a larger example if you convert decimal 200 to binary code

200=128+64+8=2⁷+ 2⁶+ 2³=11001000

Once you are happy and pleased with the process you can easily rely on the binary to decimal calculator like the one on windows.

This will convert binary numbers to decimal

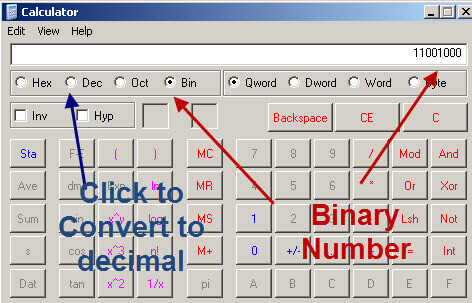
and this converts decimal numbers to binary

Understanding Hexadecimal Numbers

Take another example a hexadecimal number (base 16) will require 4 bits and has a maximum value of 15. It relies the symbols like 0-9,A,B,C,D,E,F.

They can be represented in binary form such as:

0000=0
0001=1
0010=2
0011=3
0100=4
..
1010=A
1011=B
1100=C
1101=D
1110=E
1111=F

A byte or for example 8 bits can be taken as two hexadecimal numbers.

So it stands like,

FF=binary 11111111 and decimal 255

F0=11110000 binary and decimal 240

About Post Author

Yashik Patel

Yashik Patel is a Google Certified, Digital Marketing and professional Blogger. He has 7+ years of experience in SEO, SEM, and ORM (Online Reputation Management) field.

https://bloggingdart.com